

и древних традиций
 |  | |
| Форум исследований Даосизма и древних традиций 不識浮沉寧分主客 Не распознав плывущих и тонущих, разве отделишь главных от гостей? - Чжан Бодуань | ||
|
Желая водрузить Дао Дэ за предѣлами тысячъ ли, я не боялся ни вѣтра, ни пыли, шествуя къ девяти варварскимъ народамъ. Сначала я ѣхалъ на сѣверо-западъ... | ||
| Доступ  |
德
| |||||||
Расписание занятий и стоимости:
Внимание! С сентября 2021г вводится разделение каждого Курса по стоимости на категории:
Постоянные занятия(льготная стоимость) - данную стоимость оплачивают те, кто намерен заниматься постоянно ежемесячно, без перерывов ( допускается перерыв на месяц отпуска раз в году с предупреждением как минимум за 2 месяца (60 дней) до даты начала отпуска и перерывы в случае болезней, с предъявлением справки медучреждения). В случае пропуска без 2 названных причин, занимающийся автоматически переводится на Нерегулярные занятия, с оплатой стоимости нерегулярных занятий без льгот.
Нерегулярные занятия (свободное посещение, без льгот). Для тех, кто сразу намерен заниматься с перерывами и пропусками, либо допустил пропуск Постоянных занятий. При временном сходе с Курса и попытке восстановления, установленные льготы ( в том числе парные на сходившего) не действуют, занятия возможны только по стоимостям Нерегулярных занятий (если дан допуск на участие в Курсе). Восстановиться с Нерегулярных занятий опять на Постоянные занятия можно, по заявлению практикующего, только после 8 месяцев постоянной ежемесячной практики.
| Время | Дисциплина | Стоимость |
| 12:00-13:00 | Основы Даосизма (всё о Даосизме в одном Курсе) - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 13:00-14:00 | Важнейшие термины даосизма. Дао. Исследования, трактаты, этимология, смысл. - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 14:00-15:00 | Курс Основы Этимологии иероглифов - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 15:00-15:30 | Перерыв | - |
| 15:30-16:30 | Раскрытие истины Ицзина - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 16:30-17:30 | Трактаты Школы Улюпай - "Хуэйминцзин" - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 18:00-18:45 | новый курс! Спецкурс: Даосская схема (карта) Внутреннего прохождения , Нэйцзинту 內經圖 - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| 18:45-19:30 | новый курс! Спецкурс: Внутренняя алхимия по материалам Даоцзана. Исследования академика Джозефа Нидэма. - ИДЕТ НАБОР, проводятся занятия. (4 занятия/мес.) |
|
| Время | Дисциплина | Стоимость |
| 7:15-7:55 | Спецсистема чистки кровеносных сосудов - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 8:00-9:00 | Практика Базовой Сваи - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 9:00-10:00 | Свая Ускоренного прохождения(+ к Базовое Свае) - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 10:00-11:00 | Тексты Школы Юйсяньпай - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 11:00-12:15 | Перерыв | - |
| 12:15-13:00 | Беседа "Смыслы Лаоцзы. Вечная истина Даодэцзина" - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 13:00-14:00 | Алхимия знаменитых бессмертных сяней - Чжунли Цюаня и Люй Дунбиня. Основа всех школ алхимии с начала н.э. - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 14:00-15:00 | Канон медицины Китая "Хуанди Нэйцзин" - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| 15:00-16:00 | Повторение частей отдельных пропущенных Курсов. |
|
| 16:00-17:00 | Иероглифика 2й поток (запись закрыта) |
|
| 17:00-18:00 | Синьицюань семьи Дай - основы и энергетика. - ИДЕТ НАБОР, проводятся занятия. (10 занятий (4+3+3) за 3 мес.) |
|
| Время | Дисциплина | Стоимость |
| 20:15-21:00 | новый курс! Спецкурс: Даосская схема (карта) Внутреннего прохождения, Нэйцзинту 內經圖 Для тех, кто не может посещать основной курс по субботам занятия по пятницам будут с Апреля 2024 |
|
| 12:00-13:00 | Основы Даосизма (всё о Даосизме в одном Курсе) Для тех, кто не может посещать основной курс по субботам. - ИДЕТ НАБОР, проводятся занятия. |
|
| Новости Центра «Дао Дэ» | Горячие темы | Наше видео |
| К странице... |
| Сообщение форума |
| |
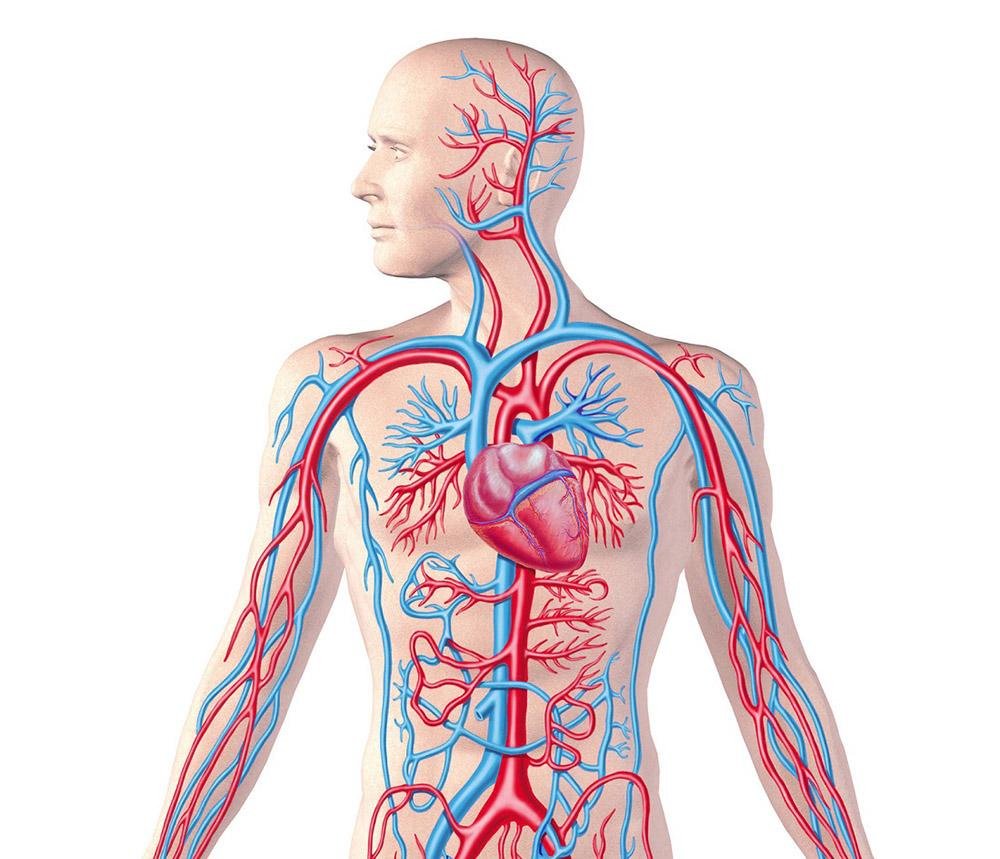
Чистка кровеносных сосудов и каналов
Чунсюэгун - это полноценная система улучшения циркуляции ци и крови в теле и органах. Позволяет очистить сосуды и снизить нагрузку на сердце. Рекомендована тем, кто ведет малоподвижный образ жизни (застой крови) или просто хочет чувствовать своё тело легким и подвижным.
На первом этапе важно активизировать органы кроветворения. Для этой цели служат 2 первых упражнения. Воздействуя на кости таза и внутренние органы, добиваются улучшения и отладки функций кроветворения.
Постепенно у практикующих появляется способность "второго сердца" которая позволяет дополнительно прокачивать кровь по телу

Столбовое стояние (Свая)
Курс Чжуангун - это метод насыщения тела и духа энергией ци.
C древности и по сей день Величайшие Мастера Китая используют этот метод совершенствования себя для сбора ци и проявления скрытых способностей человека.
Этот курс подойдет если энергии постоянно "не хватает на самое важное".
Чего можно добиться с помощью метода Чжуангун (Сваи):
Главное требование - регулярная ежедневная практика. Обычно это 40 мин - расслабления, настройки тела и ума, 20 мин — набора ци.
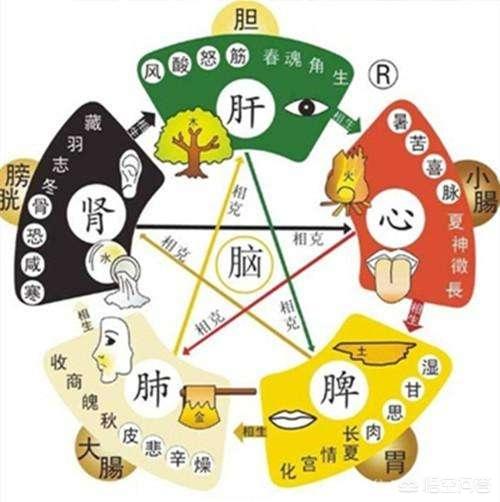
Схема элементов и соответствий человека и внешнего мира
Всё о Даосизме в одном Курсе. Курс рекомендован каждому, кто интересуется искусством взращивания жизни, уже занимается практикой или впервые хочет познакомиться с древним учением, на котором строится вся китайская цивилизация.
Главные принципы Курса:

Эволюция иероглифа Дао
Исследования, трактаты, этимология и смысл.
Курс последовательно раскрывает изначальный смысл понятия Дао:
На эти вопросы вы получите ответы на данном курсе.


Беседы Чжунли Цюаня и Люй Дунбиня
Данный Курс — Особый. Здесь изучаются трактаты 2х самых известных Бессмертных-Сяней Китая — Чжунли Цюаня и Люй Дунбиня. Эти тексты действительно превосходны для развития даосского мировоззрения и понимания многих важных основ даосизма и алхимии.
Мы изучим все их главные тексты — «Линбао бифа», «Чжунлюй чуаньдао цзи», «100 иероглифов», «Книгу указания тайны» и т.д.
Содержание трактатов чрезвычайно обильно важнейшими знаниями — порядком практики алхимии, ее уровней, закономерностей Инь Ян, Неба и Земли и т.д.
Хороших переводов данных текстов до сих пор все еще нет…
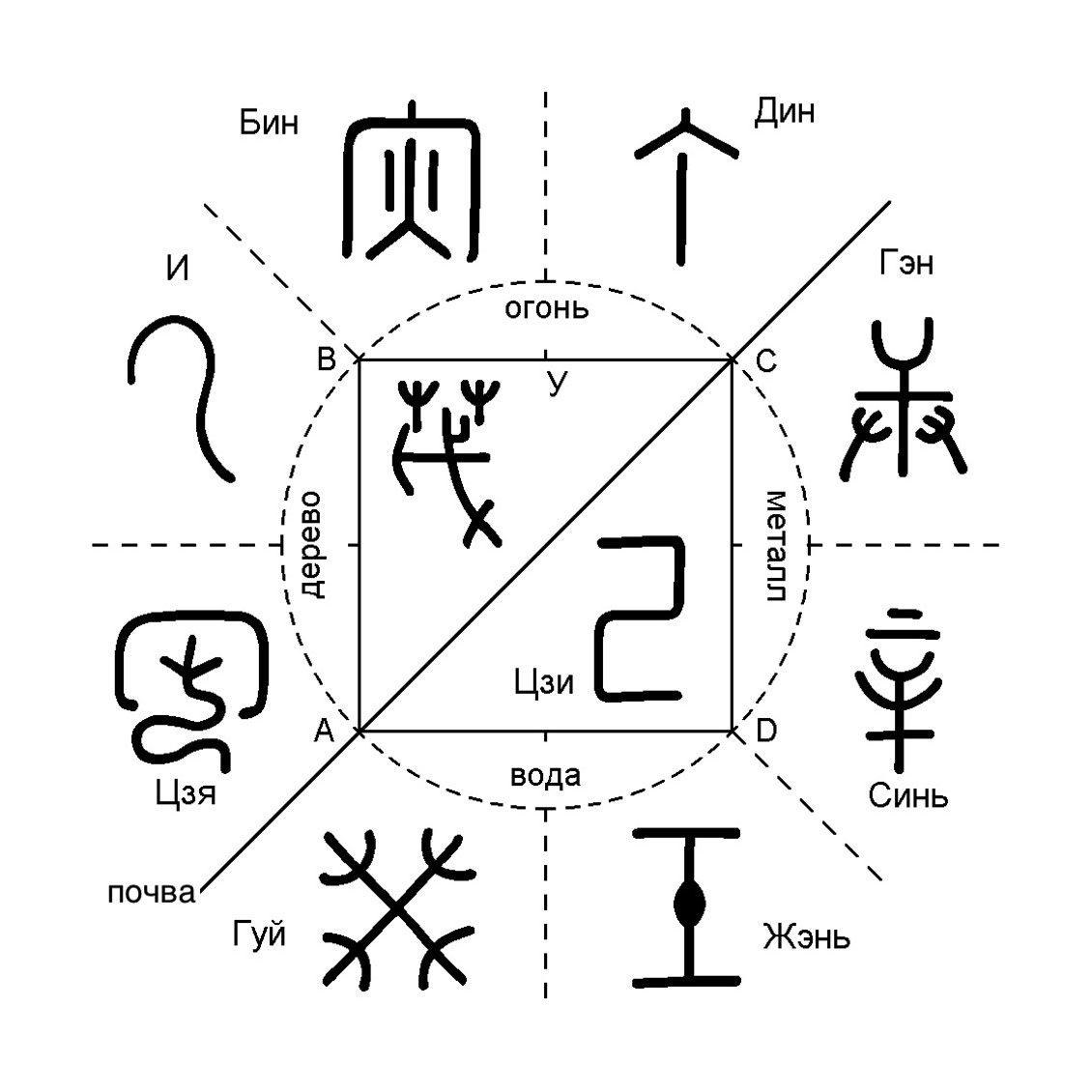
12 циклических знаков и их древние формы
Этимология – это способ проникнуть к самому корню цивилизации-долгожителя без необходимости овладения древнекитайским языком. Это возможность прикоснуться к смыслам заложенным древними мудрецами более 5000 тысяч лет назад. Для участия на курсе не требуется специальная подготовка и даже знание китайского языка!
Курс начинается с изучения трудов по этимологии авторов Леона Вигера и Жака-Андрэ Лавье, написавших множество книг по китайской культуре, даосизму, буддизму и китайскому языку.
Что можно получить от данного курса:

Связь триграмм Цянь и Кунь
Все когда-нибудь впервые слышат о Великой Книге Перемен (Ицзин). В этой книге описано само устройство вселенной и тем, кто постиг её секреты - весь мир, будущее и прошлое открывается как на ладони.
-Великие используют это знание для управления собой и для практики,
-Средние используют это знание для управления государством и подданными,
-Низшие используют это знание для гадания и выбора для себя удачных дней.
Однако безусловно все стремятся разгадать тайны скрытые в данном тексте.
Даос-отшельник Лю Имин по прозвищу "Постигнувший изначальное" в своем трактате "Раскрытие Истины Ицзин" не скрывает тайн даосизма от непосвященных и прямо излагает все важнейшие принципы и сложные места Ицзина и алхимии. Поистине такое сочетание двух тайных доктрин даосизма в одном связанном разъяснении — огромный подарок для любого стремящегося понять тайны даосской алхимии и науки Перемен!








